Osová souměrnost
30. 09. 2021
Úvod do problematiky:
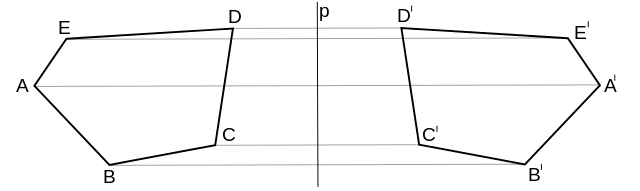
Osová souměrnost je dána přímkou o a přiřazuje každému bodu X mimo osu takový bod X´, že přímka o je osou úsečky XX´. Jinými slovy: obraz má od osy stejnou vzdálenost jako původní bod a spojnice bodů je kolmá na osu. Osová souměrnost zachovává vzdálenosti i úhly, jde tedy o druh shodnosti.
Osově souměrný útvar
Útvar označujeme za osově souměrný, pokud je v nějaké osové souměrnosti obrazem sebe sama. Osu této souměrnosti pak nazýváme osou útvaru.
Příklady osové souměrnosti:
- Úsečka je osově souměrná a má v rovině jedinou osu souměrnosti – kolmici v jejím středu.
- Rovnoramenný trojúhelník je osově souměrný – osa prochází jedním jeho vrcholem a středem základny.
- Všechny pravidelné mnohoúhelníky jsou osově souměrné. Počet os souměrnosti je roven počtu vrcholů daného mnohoúhelníku.
- Kruh je osově souměrný a má nekonečně mnoho os souměrnosti.
Příklady na procvičení:
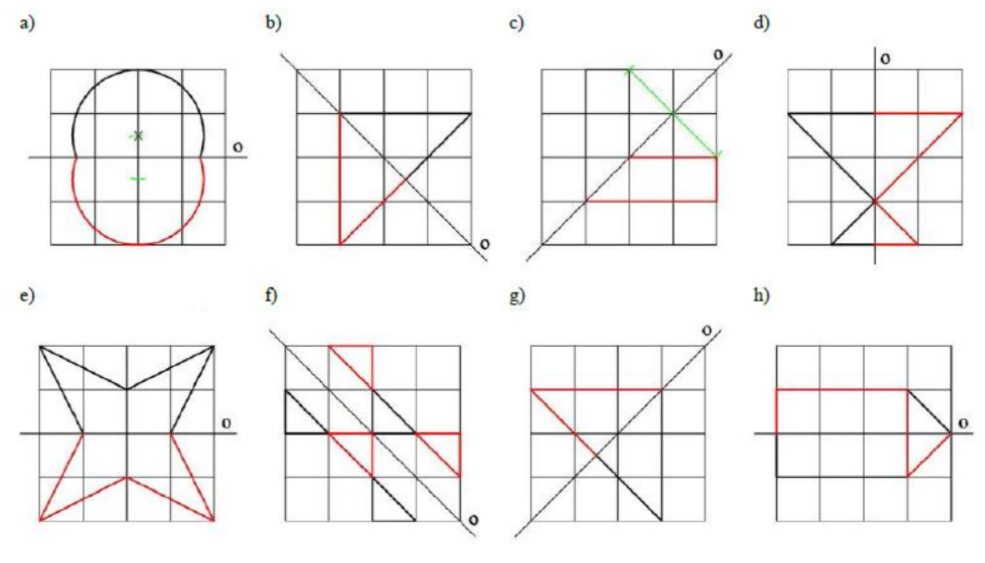
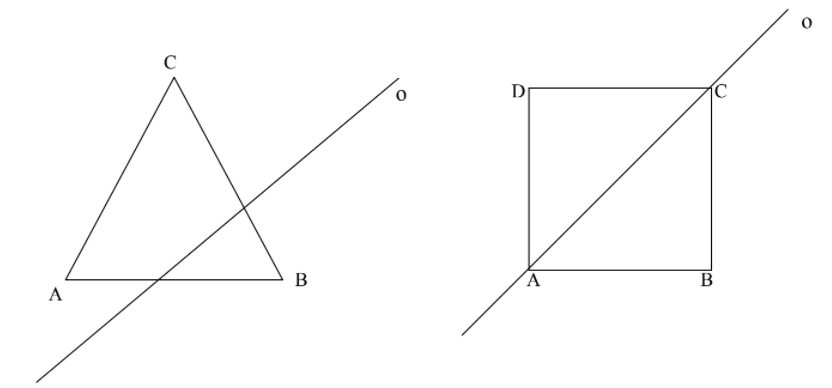
- Sestroj osově souměrné obrazce podle daných os:
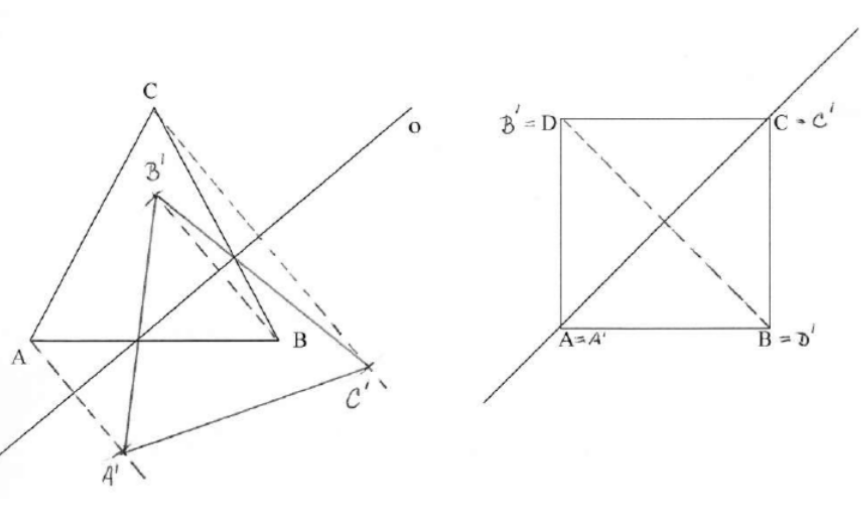
Výsledky příkladu 1:
- Dokresli ornamenty ve čtvercové síti podle osy souměrnosti o:
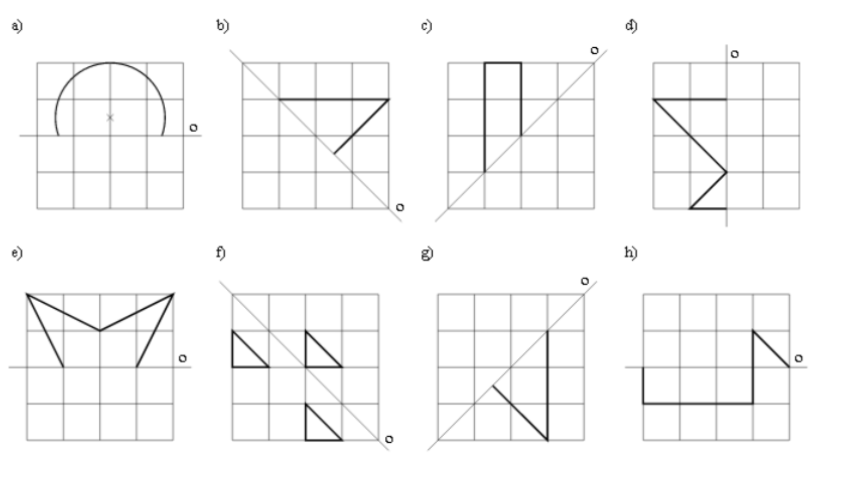
Výsledky příkladu 2: